현재까지 발견된 이 책의 오탈자 정보와 오류, 그리고 보다 매끄러운 문장을 위해 수정한 내용을 안내해드립니다. 번역과 편집 시에 미처 확인하지 못하고 불편을 끼쳐드려 죄송하다는 말씀을 드립니다. 아래의 오탈자 사항은 추후 재쇄 시에 반영하도록 하겠습니다.
이외의 오탈자 정보를 발견하시면 옮긴이(evion12@gmail.com)나 출판사(help@jpub.kr)로 연락해 주시면 고맙겠습니다.
최종수정일자: 2024년 6월 4일
6쇄본 오탈자
(업데이트 순)
6쪽 세 번째 문단 2행에서(김O민 님 제보)
x에 대해는 ==> x에 대해서는
12쪽 그림 1.7 제목 2행에서(김O민 님 제보)
18일 경우고 ==> -18일 경우고
24쪽 하단의 '토마스 베이즈' 인물 설명 상자 우측 문단 4-5행에서(김O민 님 제보)
‘Philosophical Transactions of the Royal Society’에 개제된
==>
‘Philosophical Transactions of the Royal Society’에 게재된
26쪽 1-2행에서(김O민 님 제보)
집합을 L개 만들 수 있다 ==> 집합을 L개 만들 수 있다.
33쪽 5-6행에서(김O민 님 제보)
이 과정에서 이 둘은 w와 관련이 없기 때문에 식 1.62 오른쪽 변의 마지막 두 항을 제외할 수 있다.
==>
이 과정에서 식 1.62 오른쪽 변의 마지막 두 항은 w와 관련이 없기 때문에 제외할 수 있다.
35쪽 4-5행에서(김O민 님 제보)
예측 분포가 다음의 식 1.69와 같이 가우시안 분포로 주어진다는 것을 알 수 있다.
==>
예측 분포는 다음의 식 1.69와 같이 가우시안 분포 형태로 표현된다는 것을 알 수 있다.
38쪽 10-11행에서(김O민 님 제보)
'x'가 새로운 관측값의 예시다.
==>
'×'가 새로운 관측값의 예시다.
(참고: 영어 x가 아니라 지점을 표시하는 × 기호입니다)
56쪽 마지막 문단 4-5행에서(김O민 님 제보)
N개의 동일한 물체가 몇 개의 통 안에 담겨 있다고 가정해 보자.
==>
N개의 동일한 물체를 몇 개의 통 안에 담는다고 가정해 보자.
89쪽 2행에서(김O민 님 제보)
대칭성을 띤다고 말할 수 있다.
==>
대칭성을 띤다고 말할 수 있다. 다음은 공분산 행렬의 고유 벡터 방정식을 고려해 보자.
95쪽 3-4행에서(김O민 님 제보)
하지만 앞에서의 사례와 마찬가지로 분포에 대한 구조를 구조를 모델에 도입함으로써 다룰 수 있는 복잡도가 되었다.
->
이 역시 앞에서의 사례와 마찬가지로 분포에 대한 구조를 도입함으로써 다룰 수 있는 복잡도의 모델이 되었다.
427쪽 식 8.35에서 수식 변경(김O민 님 제보)

==>

427쪽 식 8.36 아래 문장에서(김O민 님 제보)
따라서 다항 계수 w가 주어졌을 때 에 대한 예측 분포는
==>
다항 계수 w가 주어졌을 때 \hat{t}에 대한 예측 분포는
(참고: \hat{t}은 아래 모습과 같습니다.)

437쪽 4번째 줄 (김O민 님 제보)
이때 는 양의 상수다. ==> 이때 \eta는 양의 상수다.
(참고: \eta는 아래 모습과 같습니다.)

455쪽 식 8.64 아래 문장에서 x를 이탤릭체로 변경(김O민 님 제보)
변수 노드 x로의 메시지로 볼 수 있다.
==>
변수 노드 x로의 메시지로 볼 수 있다.
484쪽 맨 밑에서 5-6행에서(김O민 님 제보)
이는 각각 원 이미지와 대조해서 4.2%, 8.3%, 16.7%의 압축률에 해당한다.
==>
이는 각각 원본 이미지 대비 4.2%, 8.3%, 16.7%의 압축률에 해당한다.
485쪽 식 9.7 아래 문장 1행에서 z 모양 변경(김O민 님 제보)

==>

486쪽 식 9.12 아래 문장 1행에서(김O민 님 제보)
가우시한 혼합 ==> 가우시안 혼합
492쪽 세 번째 문단 10행에서(김O민 님 제보)
M단계에서는 식 9.17, 식 9.19, 식 9.22를 이용해서 확률값, 공분산 값, 혼합 계숫값들을
==>
M단계에서는 식 9.17, 식 9.19, 식 9.22를 이용해서 평균값, 공분산 값, 혼합 계숫값들을
497쪽 4행에서(김O민 님 제보)
정의된 모델인 경우 ==> 정의된 모델에 대한
501쪽 3행에서(김O민 님 제보)
이산 이산 확률 변수들의 ==> 이산 이진 확률 변수들의
505쪽 3행에서(김O민 님 제보)
다항 이산 변수에 ==> 다항 이진 변수에
513쪽 6행에서(김O민 님 제보)
최대점에 도달한 것 ==> 최대점에 도달한 것과 같다.
524쪽 그림 10.2 제목 2행에서(김O민 님 제보)
빨산색 경로는 ==> 빨간색 경로는
526쪽 2행에서(김O민 님 제보)
여기서 그들은 ==> 여기서 이것들은
529 쪽그림 10.4 제목의 2-3행에서(김O민 님 제보)
(b) 재추정 후의 인자 q_\mu(\mu) ==> 인자 q_\mu(\mu)를 재추정한 후
(c) 재추정 후의 인자 q_\tau(\tau) ==> 인자 q_\tau(\tau)를 재추정한 후
533쪽 식 10.43 아래 1행에서(김O민 님 제보)
식 10.41의 분해를 사용하였다.
==>
이제 식 10.41의 분해를 사용할 것이다.
537쪽 식 10.67 아래 1행에서(김O민 님 제보)
최대 가능도 EM에서의 확률값에 대한 해당 결과와 비슷하다.
==>
최대 가능도 EM에서의 책임값에 대한 해당 결과와 비슷하다.
541쪽 식 10.78 아래 2행에서(김O민 님 제보)
다음을 얻게 된다
==>
다음을 얻게 된다.
572쪽 8행에서(김O민 님 제보)
바탕으로하고 있다. ==> 바탕으로 하고 있다.
579쪽 밑에서 2행에서(김O민 님 제보)
모았다. ==> 보았다.
589쪽 3행에서(김O민 님 제보)
모든 부값들이 ==> 모든 부모의 값들이
599쪽 밑에서 2해에서 공백 하나 줄임(김O민 님 제보)
추정 사후 분포를 ==> 추정 사후 분포를
602쪽 식 11.30 아래 문장의 식 중에서(김O민 님 제보)

==>
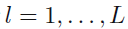
603쪽 11.2절 두 번째 문단 3행에서(김O민 님 제보)
이때 표본의 순차적인 배열 z^(1), z^(2), ... 마르코프 연쇄의 형태를 가진다.
==>
따라서 표본의 순차적인 배열 z^(1), z^(2), ... 은 마르코프 연쇄의 형태를 가진다.
603쪽 11.2절 두 번째 문단 6행에서(김O민 님 제보)
알고리즘의 각 반복 단계에서 사후 분포로부터 후보 표본
==>
알고리즘의 각 반복 단계에서 제안 분포로부터 후보 표본
608쪽 첫 번째 문단 밑에서 2행에서(김O민 님 제보)
만약 분포가 다양해지는 길이 척도가
==>
만약 분포가 달라지는 길이 척도가
620쭐 본문 3행에서(김O민 님 제보)
토끼뜀 단계를 ==> 도약 단계를
620쪽 6행, 620쪽 식 11.68 밑 2행, 620 밑에서 2행에서 R 서체를 \mathcal{R}로 변경(김O민 님 제보)
R ==> R
684 2행, 684쪽 5행, 684쪽 밑에서 1행, 690쪽 마지막 문단 1행(2개), 690쪽 마지막 문단 4행, 697쪽 식 13.43 아래 6행에서 그리스 문자 변경 (김O민 님 제보)

==>
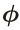
684쪽 밑에서 2행에서(김O민 님 제보)
초첨을 ==> 초점을
689쪽 식 13.14 아래 3행에서(김O민 님 제보)

==>
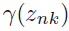
690쪽 밑에서 마지막 문단 4행, 747쪽 1-2행(김O민 님 제보)
책임도 ==> 책임값
698쪽 밑에서 1행에서(김O민 님 제보)
사전 분포의 로그를 추가해야 ==> 사전 분포 p(\theta)의 로그를 더해야
(참고: p(\theta)는 아래 기호임)

699쪽 13.2.3절 3행에서 맨 앞 공백 제거(김O민 님 제보)
이 알고리즘은
==>
이 알고리즘은
711쪽 밑에서 5번째 줄(김O민 님 제보)
관측값 x_1, ..., x_N이 주어졌을 때의 z_n 사후 확률을 나타내는 값
==>
관측값 x_1, ..., x_{n-1}이 주어졌을 때의 사후 확률 z_{n-1}을 나타내는 값
712쪽 7-8행에서(김O민 님 제보)
가우시안 K개의 혼합 분포로
==>
K개 가우시안 분포의 혼합 분포로
712쪽 세 번째 문단 3행에서(김O민 님 제보)
Kalmsn ==> Kalman
716쪽 세 번째 문단 1행에서(김O민 님 제보)
바로 관측이다. ==> 바로 추적이다.
719쪽 식 13.109 아래 2행에서(김O민 님 제보)
최초 매개변수 ==> 먼저 매개변수
723쪽 식 13.121 밑 2행에서 이탤릭체로(김O민 님 제보)
성분 l을 ==> 성분 l을
최종수정일자: 2022년 2월 10일
5쇄본 오탈자
(업데이트 순)
579쪽 네 번째 문단 3행에서(정O택 님 제보)
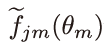
==>
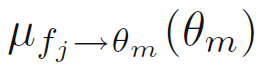
554쪽 식 10.130에서(정O택 님 제보)
==>

555쪽 첫 줄에서(정O택 님 제보)
그림 10.129로부터 ==> 식 10.129로부터
식 10.134와 식 10.135 사이 문단 두 번째 행에서(정O택 님 제보)
볼록 함수를 얻게 된다. 로그를 취한 형태가 볼록 함수라는 것은
==>
오목 함수를 얻게 된다. 로그를 취한 형태가 오목 함수라는 것은
584쪽 10.31번 문제 두 번째 행에서(정O택 님 제보)
x^2에 대해서는 오목 함수임을 ==> x^2에 대해서는 볼록 함수임을
442쪽 첫 번째 문단 2~3행에서(정O택 님 제보)
동일한 네개의 변수에 대해서 같은 조건부 독립성들을 표현하는 비방향성 그래프는 존재하지 않는다.
==>
동일한 네 개의 변수에 대해서 같은 조건부 독립성들을 표현하는 방향성 그래프는 존재하지 않는다.
444쪽 아래에서 두 번째 문단 3행에서(정O택 님 제보)
K_N개 존재하게 된다. ==> K^N개 존재하게 된다.
468쪽 두 번째 문단 4행에서(정O택 님 제보)
우리는 변수 x_1,..., x_M 중 어떤 것이 최댓값을 주었는지 기록한다.
==>
우리는 변수 x_1,..., x_M 중 어떤 값들이 최댓값을 주었는지 기록한다.
최종수정일자: 2021년 2월 18일
4쇄본 오탈자
(업데이트 순)
390쪽 밑에서 일곱, 여섯 번째 줄
자동적인 연관성 결정 ==> 자동 연관도 결정
395쪽 위에서 여섯 번째줄
aparse ==> sparse
399쪽 식 7.122 바로 밑 줄의 표적값
tnk ==> t_{nk} (* 2개 다)
400쪽 위에서 두 번째줄
K3 ==> K^3
xx쪽 아홉 번째 줄 (박*성 님 제보)
이와 비슷하게 (a,b) ==> 이와 비슷하게 [a,b)
126쪽 5행에서 (박*영 님 제보)
기댓값 최적화(expectation maximization)라는
==>
기댓값 최대화(expectation maximization)라는
278쪽 5.3.4절 4행에서 (박*영 님 제보)
네크워크상의 ==> 네트워크상의
278쪽 5.3.4절 3행에서 (박*영 님 제보)
야코비한 행렬의 ==> 야코비안 행렬의
279쪽 (식 5.73) 윗문단 2행에서 (박*영 님 제보)
야코비한 행렬을 ==> 야코비안 행렬을
280쪽 (식 5.76) 아래 문단 1행에서(박*영 님제보)
야코비한 행렬을 ==> 야코비안 행렬을
280쪽 (식 5.76) 아래 문단 3-4행에서(박*영 님제보)
야코비한 행렬의 ==> 야코비안 행렬의
352쪽 두 번째 문단 1행에서(박*영 님 제보)
ARM 체계는 ==> ARD 체계는
399쪽 그림 7.2 제목 3행에서 (박*영 님 제보)
훨신 ==> 훨씬
432쪽 첫 번째 문단 4행에서 (박*영 님 제보)
훨신 ==> 훨씬
498쪽 (식 9.36) 아래 첫 번째 문단 3행에서 (박*영 님 제보)
훨신 ==> 훨씬
662쪽 1행에서 (박*영 님 제보)
훨신 ==> 훨씬
739쪽 12행에서 (박*영 님 제보)
훨신 ==> 훨씬
350쪽 세 번째 문단 4행에서 (박*영 님 제보)
완벽환 주변화는 ==> 완벽한 주변화는
478쪽 두 번째 문단 1행에서 (박*영 님 제보)
가우시안 혼압 분포는 ==> 가우시안 혼합 분포는
482쪽 세 번째 문단 1행에서 (박*영 님 제보)
K-메도이드(`) 알고리즘이다.
==>
K-메도이드(K-medoids) 알고리즘이다.
162쪽 마지막 문단 1행에서 (박*영 님 제보)
전체 데이트 포인트를
==>
전체 데이터 포인트를
305쪽 식 5.144와 그 아래 줄에서 (박*영 님 제보)
==>
164쪽 식 3.28 아래 1행에서(박*영 님 제보)
이는 식 3.15의 최조 제곱 해를 간단히 확장한 형태다.
==>
이는 식 3.15의 최소 제곱 해를 간단히 확장한 형태다.
267쪽 3행에서(박*영 님 제보)
지역적 최소점(local mimima)이라고
==>
지역적 최소점(local minima)이라고
37쪽 식 1.73 아래 문단 두 번째 줄(박*영 님 제보)
베이지안 정보 기준(Bayseian information criterion, BIC)
==>
베이지안 정보 기준(Bayesian information criterion, BIC)
386쪽 마지막 문단 첫 번째 줄(박*영 님 제보)
PAC 베이지안(PAC-Bayseian)
==>
PAC 베이지안(PAC-Bayesian)
395쪽 두 번째 문단 네 번째 줄(박*영 님 제보)
순차적 희박 베이지안 학습 알고리즘(sequential aparse bayseian learning algorithm)
==>
순차적 희박 베이지안 학습 알고리즘(sequential aparse bayesian learning algorithm)
404쪽 첫 번째 문단 네 번째 줄(박*영 님 제보)
베이지안 네트워크(Bayseian network)
==>
베이지안 네트워크(Bayesian network)
819쪽 찾아보기 B에서(박*영 님 제보)
Bayseian information criterion
==>
Bayesian information criterion
819쪽 찾아보기 B에서(박*영 님 제보)
PAC-Bayseian
==>
PAC-Bayesian
825쪽 찾아보기 S에서(박*영 님 제보)
sequential aparse bayseian learning algorithm
==>
sequential aparse bayesian learning algorithm
827쪽 찾아보기 P에서(박*영 님 제보)
Bayseian network
==>
Bayesian network
144쪽 연습문제 2.7번 2행에서(박*영 님 제보)
x = 1을 m개 관찰하였고 x = 0을 l개 관찰했다고 해보자.
==>
x = 1을 m개 관찰하였고 x = 0을 l개 관찰했다고 해보자.
67쪽 연습문제 1.13번 질문에서(박*영 님 제보)
이때 실제 평균값 𝜇 대신에 최대 가능도 추정값 𝜇_ML를 사용했다고 하자.
==>
이때 최대 가능도 추정값 𝜇_ML이 실제 평균값 𝜇로 대체되었다고 가정하자.
최종수정일자: 2020년 1월 08일
3쇄본 오탈자
(업데이트 순)
313쪽 식 5.161과 5.162 사이 문장 (정*영 님 제보)
이와 비슷하게 가중치 w에 대한 사후 분포를 => 이와 비슷하게 가중치 w에 대한 사전 분포를
241쪽 마지막 줄 (박*규 님 제보)
그에 따라 f(z)의 z0에서의 미분값이 음수여야 한다
=>그에 따라 f(z)의 z0에서의 2차 미분값이 음수여야 한다.
245쪽 식 4.141 바로 아래 줄 (박*규 님 제보)
사후 분포 => 사전 분포
204쪽 일곱 번째 줄 (박*규 님 제보)
y(x)의 절댓값은 점 x와 결정 표면 사이의 수직 거리 r에 해당함을 알 수 있다.
=>
y(x)의 값은 점 x와 결정 표면 사이의 수직 거리 r에 비례함을 알 수 있다.
최종수정일자: 2019년 6월 4일
2쇄본 오탈자
(업데이트 순)
110쪽 1-2행 (박*규 님 제보)
식 2.141로 주어진 사후 분산의 평균이
=>
식 2.141로 주어진 사후 분포의 평균이
173쪽 식 3.51 다음 문단 첫 번째 줄
사전 분포가 가우시안 분포이기 때문에 => 사후 분포가 가우시안 분포이기 때문에
62쪽 아홉 번째 줄 (박*규 님 제보)
1.114로부터 오목함수 f(x)가 => 114로부터 볼록함수 f(x)가
82쪽 19번째 줄 (박*규 님 제보)
최대 공분산의 결괏값과 같아진다. 베이지안의 결괏값과 최대 공분산의 결괏값이
=>
최대 가능도의 결괏값과 같아진다. 베이지안의 결괏값과 최대 가능도의 결괏값이
81쪽 식 2.18 아래줄 (이*호 님 제보)
x = 0인 값 하나가 있는 데이터 집합 => x = 0인 값 l개가 있는 데이터 집합
52쪽 식 1.90 (이*환 님 제보)
▼
51쪽 식 1.85 (이*환 님 제보)

▼

로그 가능도가며 => 로그 가능도이며
최종수정일자: 2019년 2월 11일
1쇄본 오탈자
(업데이트 순)
95쪽 위에서 세 번째 줄
분포에 대한 구조를 구조를 모델에 => 분포에 대한 구조를 모델에
106쪽 그림 2.10 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
128쪽 쪽 마지막 줄의 수식 (조○우 님 제보)
ηM-1, 0)T => ηM-1)T
141쪽 그림 2.27 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
365쪽 그림 7.1 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
371쪽 그림 7.3 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
381쪽 그림 7.7 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
519쪽 위에서 여섯 번째 줄 (조○우 님 제보)
유한 원소법 => 유한 요소법
(* 그리고 814쪽 찾아보기의 해당 용어도 함께 수정합니다.)
576쪽 그림 10.17의 그림상의 문자 (조○우 님 제보)
기댓값 최대화 => EP
490쪽 마지막 줄 (조○우 님 제보)
비정칙 => 정칙
32쪽 그림 1.16 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
31쪽 그림 1.15 (조○우 님 제보)
(* 그림이 아래쪽 것으로 변경되어야 합니다.)
▼
서문 xx쪽의 (조○우 님 제보)
멱함수 => 범함수
(* 해당 페이지의 모든 '멱함수'를 말합니다)
'오탈자 정보' 카테고리의 다른 글
| [아마존 웹 서비스 부하 테스트 입문]_오탈자 (0) | 2018.10.11 |
|---|---|
| [코딩 교육을 위한 마이크로비트]_오탈자 (0) | 2018.10.08 |
| [송쌤의 엔트리 코딩 학교]_오탈자 (0) | 2018.09.07 |
| [웹 서비스를 만들며 배우는 node.js 프로그래밍]_오탈자 (0) | 2018.07.24 |
| [사물인터넷을 위한 ESP8266 프로그래밍]_오탈자 (0) | 2018.07.18 |